A Cartilha da Anotação Big-O
A anotação Big-O mede o pior caso de complexidade de um algoritmo. Na anotação Big-O, n representa o número de entradas. A pergunta para o Big-O é: “O que acontecerá se n aproximar do infinito?”
Quando você implementa um algoritmo, a anotação Big-O é importante para dizer a você o quão eficiente está o algoritmo.
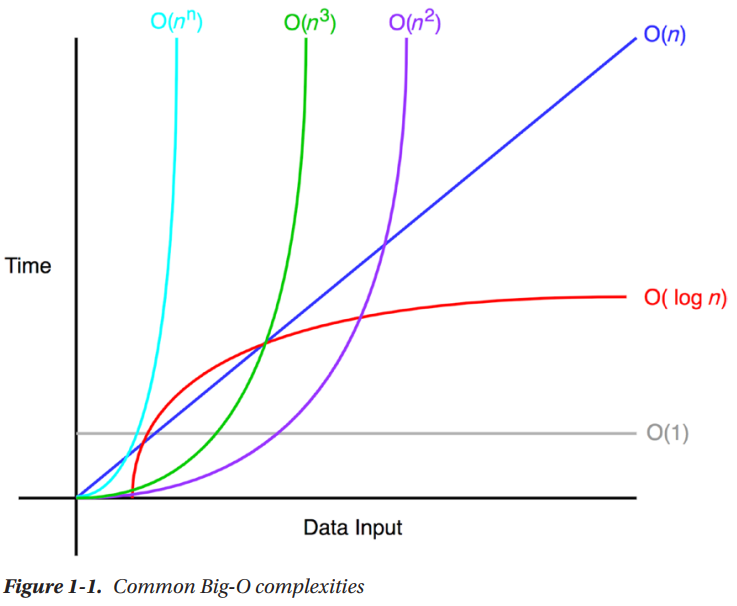
O não muda por causa do Data Input. Consequentemente, O está referenciado como sendo um tempo constante. Um exemplo de um O, é o algoritmo que está acessando um item de um array por um index. O(n) é um tempo linear e aplica para algoritmos que precisa fazer n operações dentro de um pior cenário.
Um exemplo de um O(n) é um algoritmo que está imprimindo números de 0 a n-1, veja o exemplo:
function exampleLinear(n){
for(var i = 0 ; i < n ; i++){
console.log(i);
}
}
Similarmente, O(n²) é um tempo quadrático e o O(n³) é um tempo cúbico. Veja os exemplos:
function exampleQuadratic(n){
for(var i = 0 ; i < n ; i++){
console.log(i);
for(var j = i; j < n; j++){
console.log(j);
}
}
}
function exampleCubic(n){
for(var i = 0 ; i < n ; i++){
console.log(i);
for(var j = i; j < n; j++){
console.log(j);
for(var k = j; j < n; j++){
console.log(k);
}
}
}
}
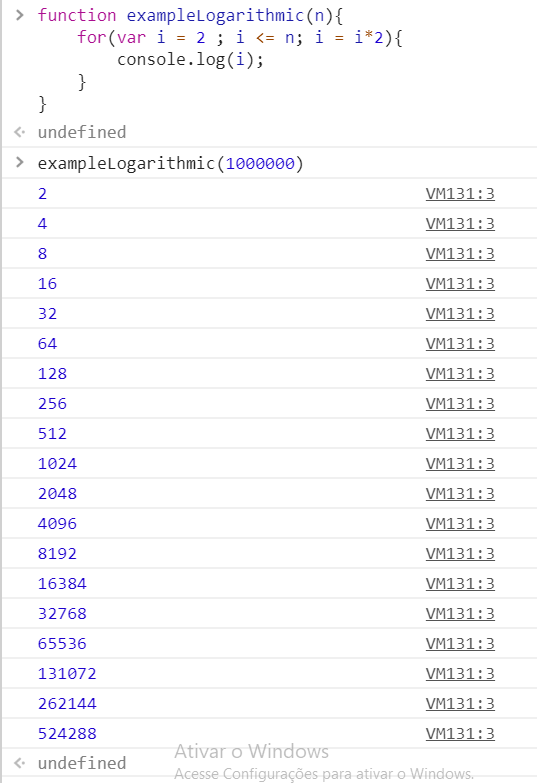
O exemplo a seguir é uma potência de 2 em 2 para n. A eficiência da complexidade do tempo algorítmico é aparentemente grande para grandes números. Apesar de n ser um milhão, exempleLogarithmic irá imprimir apenas 19 itens porque log2 (1,000,000) = 19.9315686. Veja o código: https://www.calculat.org/pt/logaritmos/logaritmo.html
Regras da Anotação Big-O
Vamos representar a complexidade de um algoritmo com f(n). n representa o número de inputs, f(n)tempo representa o tempo necessário, e f(n)espaço representa o espaço (adicional de memória) que o algoritmo precisa. O objetivo de analisar um algoritmo é entender a eficiência do algoritmo por meio do cálculo f(n). Contudo, pode ser um desafio fazer o cálculo f(n). A anotação Big-O fornece algumas regras para ajudar o desenvolvedor a resolver o cálculo f(n).
Regra do coeficiente: se f(n) é O(g(n)), então kf(n) é O(g(n)), para qualquer constante onde k>0. A primeira regra é a do coeficiente, a qual elimina coeficientes não relacionados ao tamanho do input, n. Isto porque o n se aproxima do infinito, e outros coeficientes tornam-se insignificantes.
Regra da soma: se f(n) é O(h(n)) e g(n) é O(p(n)), então f(n) + g(n) é O(h(n)+p(n)). A regra da soma simplesmente é o resultado da complexidade do tempo, que é a soma de dois tempos complexos, o resultado da anotação do Big-O é também a soma de duas diferentes anotações de Big-O.
Regra do produto: se f(n) é O(h(n)) e g(n) é O(p(n)), então f(n) x g(n) é O(h(n) x p(n)). A regra do produto é que o Big-O é multiplicado quando tempos complexos são multiplicados.
Regra transitiva: se f(n) é O(g(n)) e g(n) é O(h(n)), então f(n) é O(h(n)). A regra transitiva é um simples caminho que ao mesmo tempo a complexidade tem o mesmo Big-O.
Regra polinomial: se f(n) é um polinomial de grau K, então f(n) é O(n^k). A regra do polinomial é quando complexidade de tempo tem o mesmo grau polinomial do Big-O.
Regra da potência do Log: log(nk) é O(log(n)) para qualquer constante onde K>0. Com a regra da potência, constantes dentro da função log são ignoradas pela anotação Big-O.
As três primeiras regras e a polinomial são as mais utilizadas.
#javascript




Deixe um comentário