Regra do Produto: “Multiplicar Big-OS”

A regra produto simplifica o estado de como o Big-Os pode ser multiplicado.

Se f(n) é O(h(n)) e g(n) é O(p(n)), então f(n)g(n) é O(h(n)p(n)).

A seguir o bloco de código demonstra uma função com dois laços de for aninhado o qual a regra produto está aplicada:

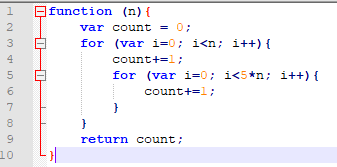
Nesse exemplo, f(n) = 5n*n porque na linha 7 executa 5n vezes para um total de n interações. Além disso, isso resulta em um total de 5n^2 operações. Aplicando a regra do coeficiente, o resultado é O(n)= n^2.

Regra do Polinomial: “Big-OS para o Poder do K”

A regra de estado do polinomial tem as complexidades de tempo.

Se f(n) é um polinomial de grau k, então f(n) é O(n^k).

A seguir o bloco do código tem apenas um laço de loop de complexidade de tempo quadrático:

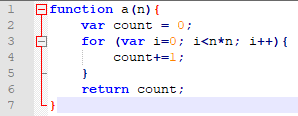
Nesse exemplo, f(n) = n^2 porque a linha 4 executa interações n*n.

Fonte: JavaScript Data Structures and Algorithms: An Introduction to Understanding and Implementing Core Data Structure and Algorithm Fundamentals (English Edition)